0. Abstract (번역)
적대적인 과정을 통해 생성 모델을 평가하는 새로운 프레임워크를 소개한다. 그 생성모델에서 우리는 동시에 두 가지 모델을 학습시켰다 : 생성모델 G (데이터 분포를 포착함) 그리고 구별하는 모델 D (샘플이 G로부터 온게 아니라 학습데이터로부터 왔는지에 대한 가능성을 측정). G에 대한 트레이닝 절차는 D가 실수를 할 확률을 최대화 한다. 이 프레임워크는 두명의 선수가 minmax게임을 하는 것에 해당한다. 독단적인 영역 함수인 G와 D에서, G는 트레이닝 데이터 분포와 D를 어디에서나 1/2이 되도록 근사(recovering)한다. G와 D가 multilayer perceptron에 정의되는 경우에, 전체 시스템은 backpropagtion에 의해 학습될 수 있다. Markov Chain(기존에 생성모델에서 요구가 되었던)또는 등록되지 않은 근접 추론 네트워크는 생성 혹은 학습 시에 필요하지 않다. 실험은 생성된 샘플에 대해 정량적이고 정성적인 평가의 잠재성을 증명했다.
1. Introduction (모르는 것 정리)
- piecewise linear unit : 구간이 나눠져 있는 선형 함수, 대표적으로 RELU
- random noise : literally하게 '잡음'을 의미함
- approximate inference : 우리의 목적은 data가 주어졌을 때의 확률을 구하는 건데 이건 정확한 값을 구하기가 너무 어렵다..그래서 그나마 비슷한 값인 P(Z|D)를 구해보자는 것이 Approximate Inference이다.
- marginalization (주변화)
- 동시확률이 주어졌을 때, 주목하지 않는 쪽의 확률변수가 취할 수 있는 모든 값에 대해 동시 확률을 계산하고 그 합을 취하는 것 => 결과적으로 얻는 확률을 주변확률 이라고 한다.
- Pr(A,B) 로 부터 Pr(A)와 Pr(B)를 알아내는 연산
- 여러 확률변수에 대한 joint*(joint probability distrubution)를 알 때, 특정 변수에 대한 분포를 주변확률분포(marginal probability distribution)라고 한다.
- Latent variable (잠재 변수)
- marginalization (주변화)
요인분석에 대해서 먼저 간단하게 설명해보면,
요인분석은 수많은 변수들 중에서 잠재된 몇 개의 변수(요인)을 찾아내는 것이다.
이 설명만 듣고 이해가 된다면 아마도 천재가 아닐까?? 아래에서 예를 들어 설명해야겠다.
학생들의 시험 성적 데이터를 예를 들어 생각해보자.
이 데이터가 수학, 과학, 영어, 중국어, 독어, 작곡, 연주 의 점수(0점-100점)으로 구성되어 있다고 하면,
수학, 과학은 상관관계가 있을 것이고 (수리계산능력)
영어, 중국어, 독어 가 상관관계가 있을 것이고 (외국어능력)
작곡, 연주 가 상관관계가 있을 것이다. (음악적능력, 음악적재능)
(위의 가정이 좀 이상할 수 있지만, 그냥 그렇다고 받아들이자...)
즉, 원래 7개의 변수(과목)으로 구성되어있지만, (그냥 봐서는 잘 모르지만 상관관계를 따져보면)
내부적으로는 3개의 잠재변수 즉, [수리계산능력], [외국어능력], [음악적재능] 으로 구성된 것으로 파악할 수 있다.
이렇게 원래 많은 수(7개)의 변수들을 소수의 몇 개의(3개)의 잠재된 변수로 찾아내는 것을 요인분석이라고 한다. 감이 오겠지만 ... 요인분석은 데이터 축소(Data Reduction)과 관계가 있다.
이렇게 찾은 잠재변수를 영어로는 Latent Variable 이라고 부른다.
출처 : https://ai-times.tistory.com/112- Latent Space ( 잠재 공간)
- 유용한 Featrue들의 분포 공간
2. Related work (모르는 것 정리)
- partition function
- 에너지가 시스템의 상태들간에 어떻게 분배되어 있는가를 나타내는 함수(통계물리학)
- Auto-encoding variational Bayes (VAE)
- Implicit(간접적) 방식
- 어떤 model에 대해 틀을 명확히 정의하는 대신 확률 분포를 알기 위해 sample을 뽑는 방법.
- e.g.) Markov Chain
- e.g.) GAN
- 어떤 확률 모델(density)을 굳이 명확히 정의하지 않아도 모델(generator) 자체가 만드는 분포로 부터 sample을 생성할 수 있음
- 어떤 확률 모델(density)을 굳이 명확히 정의하지 않아도 모델(generator) 자체가 만드는 분포로 부터 sample을 생성할 수 있음
- 어떤 model에 대해 틀을 명확히 정의하는 대신 확률 분포를 알기 위해 sample을 뽑는 방법.
- Monte Carlo approximations
- 근사의 한 방법으로, 무작위로 많이 샘플을 뽑아서 분포를 유추해보자는 아이디어
- variational approximation
- logpmodel(x;θ)을 직접 계산하기가 어렵다면 하한(lower bound)을 구하는데 이를 우리가 알고 있고 계산이 편한 모델로 대체한 다음 이 하한에 해당하는 부분을 최대화하는 방식으로 문제를 우회하자는 것-
- 출처 : https://jaejunyoo.blogspot.com/2017/04/auto-encoding-variational-bayes-vae-1.html
- Implicit(간접적) 방식
3. Adversarial nets (모르는 것 정리 및 수식 스스로 해석하도록 노력해보기)
- Input noise variables
- 여기서 noise 란? 진짜 noise를 의미함. 말그대로 noise가 input으로 들어간다.

적대적 모델링 프레임워크는 가장 간단한 방식인 multilayer perceptron이 적용되었다.

: Probability of g (데이터 x 에 대한 generator의 분포를 학습하기 위한 것)

: input noise variable. prior라고도 칭함 (Probability of z. z에 대한 분포)

: multilayer perceptron에서의 파라미터 (Paremter Theta of g. Generator의 파라미터 )

: data space에 대한 매핑을 표현. G는 미분가능한 함수.
미분가능한 함수 G는 input으로 z(노이즈). Theta g(multilayer perceptron에서의 파라미터)를 받는구나

: 두번째 multilayer perceptron. output은 single scalar

: Probability of x (데이터 x에 대한 분포)
우리는 D를 학습시켜서 학습 examples와 G로부터 나온 samples에 대해 알맞은 label을 할당하는 것을 최대화가 되게 할것이다.
우리는 동시에 G를 학습시켜서 로그값을 최소화가 되개 할 것이다.
나혼자 해석해보는 수식

: 1 - D((G에 input noise를 넣었을 때의 data space에 대한 매핑)으로 부터 나온 sample)에 대한 분포


: 데이터 x에 대한 기대값 E는, 데이터 x(두번째 multilayer perceptron의 결과 값에 관한 분포)에 대한 확률, ~에 근사한다. 즉 데이터 x를 넣었을 때의 D(x)의 결과에 대한 확률의 기댓값 이다. 그니까 원본 데이터를 D에 넣어 구별하는 것의 확률의 기댓값

: 데이터 z에 대한 기대값 E는 데이터 z(1 - D((G에 input noise를 넣었을 때의 data space에 대한 매핑)으로 부터 나온 sample)에 대한 분포), ~에 근사한다. 즉 G에 input noise 를 넣었을 때의 data space에 대한 매핑으로 부터 나온 분포를 다시 D의 input으로 넣은 결과를 최대 확률에서 뺐을 때의 확률의 기댓값 이다. 왜 최대확률에서 빼는가? 앞의 D(x)와 반대되는 값을 구하기 위해서 아닐까? 즉 G에 input noise를 넣었을 때 생성된 sample을 D에 넣어 구별하는 것의 확률의 기댓값
- non-parametric : 통계학에서 모집단의 형태에 관계없이 주어진 데이터에서 직접 확률을 계산하여 통계학적 검정을 하는 분석
4. Theoretical Results

Algorithm 1
GAN을 학습시키는 미니배치 SGD. steps는 discriminator를 학습시키기 위해 적용되고, k는 하이퍼파라미터이다. 우리는 k=1을 사용했다.

: 앞서 나온 수식을 ThetaD(multilayer perceptron-D layer)에서의 파라미터 Theta의 변화량만큼 k번 반복

: ThetaG(multilayer perceptron-G layer)에서의 파라미터 Theta의 변화량만큼 training iteration만큼 반복
즉, 한 번의 Generator 를 학습시킬 때 하이퍼파라미터 k 로 Descriminator를 학습시킨다.

generator G가 고정되었을 때, 최적의 Descriminator는 왼쪽 식과 같다.
최적의 Descriminator가 무엇인지 생각해 봤을 때, 최대값이 되는 것일텐데 이에 대한 증명은 링크에서 확인할 수 있다. alog(y) + blog(1-y)가 a/a+b에서 최대가 된다는 것을 아주 쉽게 증명해놓았다!

적분에서 갑자기 x와 z가 합쳐져서 이상했는데, 그 이유는 +로 합쳐진 두 식이 각각 1/2확률일 테니까(왜냐면 G가 너무 잘 만들기 때문에 D가 원본data를 구별할 확률가 G로 만든 data를 구별할 확률이 같아서!!!) z를 x로 바꿀 수 있다고... 링크에서 확인할 수 있다! 이때의 V는 value function.

Supp는 support set으로 괄호 안의 것에 의해 다르게 바뀌는 타입변수를 모두 모은 것을 의미한다고 한다. Supp(pdata)는 data의 확률에 의해 다르게 바뀌는 모든 변수, Supp(pg)는 generator로 생성된 데이터의 확률에 의해 다르게 바뀌는 모든 변수라고 한다. 완벽하게 이해가 되지는 않지만 -ㅅ- 이것이 위의 식의 x와 z가 합쳐지게 하는 당위성이라고 한다.
Theorem 1
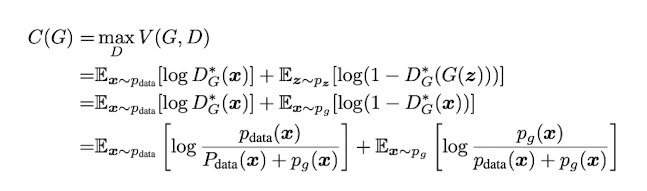
C(G)는 학습이 되게하는 기준의 최소값인데, 어떤 데이터가 g일 확률과 data(input)일 확률이 같을 때만 성립한다고 한다. 즉 G가 진짜 같은 이미지를 만들어 날때 학습이 되는 최소의 Criterion을 의미한다.
이 시점에서 C(G)는 the value - log4 이다.
밑의 Proof를 보면, 만약 Pg == Pdata일때, d위에서 구한 D*G(x)가 1/2이다. D*(G) == 1/2이면이걸 C(G)에 대입하면

log1/2 + log1/2 이므로 C(G)의 값이 -log4가 된다.
- KL 이란?
- JSD 란?
----
힘들어서 내일 마저 읽기로함..
'인공지능 > 딥러닝' 카테고리의 다른 글
| [딥러닝 파이토치 교과서] 7장 시계열 분석 Colab torchtext 오류 해결법 (0) | 2023.06.10 |
|---|---|
| [딥러닝 파이토치 교과서] ResNet 용어 정리 및 코드 분석 (0) | 2023.05.30 |
| Imagenet classification with deep convolutional neural networks 정리 (0) | 2023.03.02 |
| Transformer 공부하며 정리 (0) | 2023.02.28 |
| 신경망 학습의 전반적인 과정 (0) | 2022.12.27 |